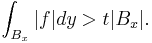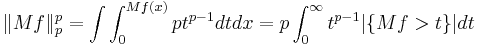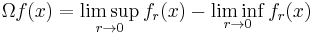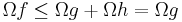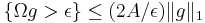Hardy–Littlewood maximal function

In mathematics, the Hardy–Littlewood maximal operator M is a significant non-linear operator used in real analysis and harmonic analysis. It takes a function ƒ (a complex-valued and locally integrable function)

f:\mathbb{R}^d \rightarrow \mathbb{C} \,

and returns a second function

Mf \,

that, at each point x ∈ Rd, gives the maximum average value that ƒ can have on balls centered at that point. More precisely,

Mf(x)=\sup_{r>0}\frac{1}{m_d(B_r(x))}\int_{B_r(x)} |f(y)|\, dm_d (y)

where

B_r(x)=\{y\in \mathbb{R}^d: \Vert y-x\Vert <r\} \,

is the ball of radius r centered at x, and md denotes the d-dimensional Lebesgue measure.

The averages are jointly continuous in x and r, therefore the maximal function Mf, being the supremum over r > 0, is measurable. It is not obvious that Mf is finite almost everywhere. This is a corollary of the Hardy–Littlewood maximal inequality

Contents

Hardy–Littlewood maximal inequality

This theorem of G. H. Hardy and J. E. Littlewood states that M is bounded as a sublinear operator from the Lp space

L^p (\mathbb{R}^d), \quad p > 1

to itself. That is, if

f\in L^p (\mathbb{R}^d),

then the maximal function Mf is weak L1 bounded and

Mf\in L^p (\mathbb{R}^d). \,

More precisely, for all dimensions d ≥ 1 and 1 < p ≤ ∞, and all ƒ ∈ L1(Rd), there is a constant Cd > 0 such that for all λ > 0, we have the weak type-(1,1) bound:

m_d \{x\in\mathbb{R}^d: Mf(x) > \lambda\} < \frac{C_d}{\lambda} \Vert f\Vert_{L^1 (\mathbb{R}^d)} .

This is the Hardy–Littlewood maximal inequality.

With the Hardy–Littlewood maximal inequality in hand, the following strong-type estimate is an immediate consequence of the Marcinkiewicz interpolation theorem: there exists a constant Ap,d > 0 such that

\Vert Mf\Vert_{L^p (\mathbb{R}^d)}\leq A_{p,d}\Vert f\Vert_{L^p(\mathbb{R}^d)}.

Subsequent work by Elias Stein used the Calderón-Zygmund method of rotations to show that one could pick Ap,d = Ap independent of d.[1][2] The best bounds for Ap,d are unknown.[2]

Proof

While there are several proofs of this theorem, a common one is given below: For p = ∞, (see Lp space for definition of L∞) the inequality is trivial (since the average of a function is no larger than its essential supremum). For 1 < p < ∞, first we shall use the following version of the Vitali covering lemma to prove the weak-type estimate. (See the article for the proof of the lemma.)

Lemma Let X be a separable metric space and 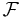\mathcal{F} family of open balls with bounded diameter. Then 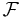\mathcal{F} has a countable subfamily \mathcal{F}' consisting of disjoint balls such that
\bigcup_{B \in \mathcal{F}} B \subset \bigcup_{B \in \mathcal{F'}} 5B
where 5B is B with 5 times radius.

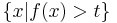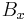Assuming the lemma for a moment, we complete the proof. For simplicity, we write |E| = m_d(E) for a measurable set E and \{f > t\} to denote the set \{ x | f(x) > t \}. If Mf(x) > t, then, by definition, we can find a ball B_x centered at x such that

\int_{B_x} |f|dy > t|B_x|.

By the lemma, we can find, among such balls, a sequence of balls B_j such that the union of 5B_j covers \{ Mf > t \}. It follows:

|\{Mf > t\}| \le 5^d \sum_j |B_j| \le {5^d \over t} \int |f|dy

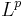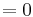This completes the proof of the weak-type estimate. We next deduce from this the L^p bounds. Define b by b(x) = f(x) if |f(x)| > t/2 and =0 else. By the weak-type estimate applied to b, we have:

|\{Mf > t\}| \le {2A \over t} \int_{|f| > t / 2} |f|dx, A = 5^d.

Then

\|Mf\|_p^p = \int \int_0^{Mf(x)} pt^{p-1} dt dx = p \int_0^\infty t^{p-1} |\{ Mf > t \}| dt

which is, by the estimate above, bounded by

2A p \int_0^\infty \int_{|f| > t/2} t^{p-2} |f| dx dt = A_p \|f\|_p^p.

where the constant 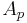A_p depends only on p and d. This completes the proof of the theorem.

Applications

Some applications of the Hardy–Littlewood Maximal Inequality include proving the following results:

Here we use a standard trick involving the maximal function to give a quick proof of Lebesgue differentiation theorem. (But remember that in the proof of the maximal theorem, we used the Vitali covering lemma.) Let 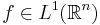f \in L^1(\mathbb{R}^n) and

\Omega f (x) = \limsup_{r \to 0} f_r(x) - \liminf_{r \to 0} f_r(x)

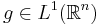where we wrote f_r(x) = {1/|B(x, r)|} \int f dy. We write f = h %2B g where h is continuous and has compact support and g \in L^1(\mathbb{R}^n) with norm that can be made arbitrary small. Then

\Omega f \le \Omega g %2B \Omega h = \Omega g

by continuity. Now, \Omega g \le 2 M g and so, by the theorem, we have:

\{ \Omega g > \epsilon \} \le (2A/\epsilon) \|g\|_1

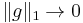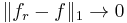Now, we can let \|g\|_1 \to 0 and conclude \Omega f = 0 a.e.; that is, \lim_{r \to 0} f_r(x) exists for almost all x. It remains to show the limit actually equals f(x). But this is easy: it is known that \|f_r - f\|_1 \to 0 (approximation of the identity) and thus there is a subsequence 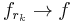f_{r_k} \to f a.e.. By the uniqueness of limit, 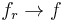f_r \to f a.e. then.

Discussion

It is still unknown what the smallest constants Ap,d and Cd are in the above inequalities. However, a result of Elias Stein about spherical maximal functions can be used to show that, for 1 < p< ∞, we can remove the dependence of Ap,d on the dimension, that is, Ap,d = Ap for some constant Ap > 0 only depending on the value p. It is unknown whether there is a weak bound that is independent of dimension.

References

  1. ^ Stein, E. M. (S 1982). "The development of square functions in the work of A. Zygmund.". Bulletin of the American Mathematical Society New Series 7 (2): 359–376. 
  2. ^ a b Tao, Terence. "Stein’s spherical maximal theorem". What's New. http://terrytao.wordpress.com/2011/05/21/steins-spherical-maximal-theorem/. Retrieved 22 May 2011.